The idea of Bloom Filter was conceived by Burton H. Bloom in 1970. In a nutshell, Bloom filter is a space-efficient probabilistic data structure normally used to check for set membership (i.e. Is element x in set S?). Bloom filter offers incredible memory and run-time savings for set membership queries with a small margin of error i.e. false positives. Bloom filter is used extensively in a variety of domains including implementing distributed system algorithms. There are over 20 variants of Bloom filter and these variations include additional capabilities such as counting, deletion, popularity awareness, false negative, and output type (boolean vs. frequency). Just to note, standard Bloom filter is susceptible to false positives, but not false negatives. In this article, we will discuss the basics of Bloom filter, different use cases, various considerations, important variations, lastly implement a Python/Go version of standard Bloom filter.
Probabilistic Data Structures
Probabilistic data structures are generally used to gain space-efficiency. They are especially useful when working with a very large dataset and trying to fit in memory. They trade in a small margin of error for considerably less storage footprint and fast processing time. Generally, the error rate can be controlled. Probabilistic data structures are streaming-friendly and can be easily parallelized. Probabilistic data structures are used to solve a variety of problems including but not limited to,
- Comparing data sets (Locality sensitive hashing /Simhash)
- Membership test (Bloom filter)
- Count-distinct problem (Cardinality estimation/HyperLogLog)
- Probabilistic Databases (BlinkDB)
- Count-min sketch (Frequency of element in stream)
- Feature hashing (Machine Learning)
For now, in this article, we will focus on Bloom filter but we will discuss the other use cases of Probabilistic data structures in upcoming posts.
Use Cases
Some really interesting use cases of Bloom filters is listed below. This is not a comprehensive but gives a good idea about the type of problems can be solved by applying Bloom Filters.
- Bitcoin uses Bloom filters to speed up wallet synchronization and also to improve Bitcoin wallet security
- Google Chrome uses the Bloom filter to identify malicious URLs - it keeps a local Bloom filter as the first check for Spam URL
- Google BigTable and Apache Cassandra use Bloom filters to reduce disk lookups for non-existent rows or columns
- The Squid Web Proxy Cache uses Bloom filters for cache digests - proxies periodically exchange Bloom filters for avoiding ICP messages
- Genomics community uses Bloom filter for classification of DNA sequences and efficient counting of k-mers in DNA sequences
- Used for preventing weak password choices using a dictionary of easily guessable passwords as bloom filter
- Similarly, Bloom filter can be used to implement spell checker using a predefined dictionary with large number of words
Standard Bloom Filter
A Bloom filter B is traditionally implemented by a single array of M bits, where M is the filter size. On filter creation, all M bits are set to 0. Also,
Bm represents a bit with index m where m ranges from [0, M − 1]. Bloom filter is then parameterized by a constant k that defines the number of hash functions. Then each hash function h0, h1, . . . , hk-1 maps an input element to an index in the range [0, M − 1]. Only insert (or add) and query operations are permitted. Delete or remove operation is not allowed in standard Bloom filters.
Insert or Add
During insert or add operation, for each element si in the set of all elements S, the bits with positions h0(si), h1(si), . . . , hk-1(si) are set to 1. Any given bit may be turned on multiple times.
Data: si is the element to insert into the Bloom filter.
Function: insert(si)
for j : 1 . . . k do
/* Loop all hash functions k
m ← hj(si);
if Bm == 0 then
/* Bloom filter had zero bit at
index m
Bm ← 1;
end
end
Query
To query for an element in the set, pass it to each of the k hash functions to get k integer array indexes. If any of the bits at these indexes are 0, the element is definitely not in the set. If all of the bits are 1, then either the element is in the set or the bits were coincidentally set to 1 by hashes of other elements, resulting in a false positive.
Data: x is the element for which membership is tested.
Function: is_member(x) returns true or false to the membership test
/* Set membership status variable t to 1
t ← 1;
j ← 1;
while t == 1 and j ≤ k do
m ← hj(x);
if Bm == 0 then
t ← 0;
end
j ← j + 1;
end
return t;
Example
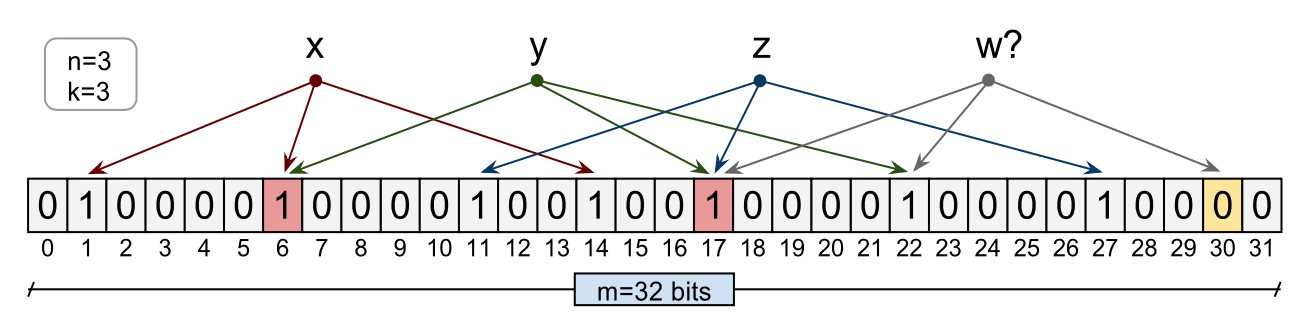
The Bloom filter illustrated below consists of a 32 bits array. Three elements have been inserted in this filter, namely x, y, and z. During the insert, each of the element has been hashed using 3 hash functions ( h1, h2 and h3) to bit indexes of the array. The corresponding bits have been set to 1. Now to query an element w which was never inserted in the bit array, element w will be hashed using the same three hash functions into bit indexes. In this case, one of the indexes is zero and hence the Bloom filter will report correctly that the element is not in the set. As you can see bit there is collision or overlap between various elements. For instance, x and y in below illustration share bit array index 6. As we insert more elements in this bit array, this overlap will increase resulting in possible false positive results. This happens when we are querying for an element which has been not inserted but due to overlapping nature of bit indexes query function matched corresponding k bits - all non-zero.
In the next illustration, we have Bloom filter with 16 bits array. MD5, SHA1 and CRC32 are used a 3 hash functions h1, h2 and h3. Four elements a, b, c, and d were inserted in the filter. After this, indexes 15, 14, 13, 10, 9, 8, 7, 5, 3 and 1 are set. Moreover, indexes 8 and 3 have collisions. When we query for q and z, the same hash functions are used. Bit indexes that correspond to q and z are examined. If the three bits for an element are set, that element is assumed to be present. In the case of q, position 0 is not set, and therefore q is guaranteed not to be present in the filter. However, z is assumed to be present since the corresponding bits have been set. We know that z is a false positive: it is reported to present though it is not actually inserted into the filter. The bits that correspond to z (positions 15, 10 and 7) were set through the addition of elements b, y and l.

False Positive Probability
The probability false positive for a membership test given that N elements of set S are inserted into a Bloom filter of M bits and k hash functions: (1 - e-kN/M)k
In order to have a fixed false positive probability, the length of a Bloom filter M must grow linearly with the N number of elements inserted in the filter while keeping the number of hash functions k constant.
Performance
A Bloom filter B requires space O(n) and can answer membership queries in O(1) time where n is number item inserted in the filter. Although the asymptotic space complexity of a Bloom filter is the same as a hash map, O(n), a Bloom filter is more space efficient (see a more detailed comparison here).
Hash functions
The hash functions used in a Bloom filter should be independent, reproducible, uniformly distributed, and as fast as possible. That said, hashing is generally slower process especially when utilizing cryptographic hashes such as MD5, SHA, etc. Reducing the number of required hashes can help to speed up the hashing process.
Kirsch et al. demonstrated that only two hash functions are necessary to effectively implement a Bloom filter without any increase in the asymptotic false positive probability. This technique is known as double hashingv and it utilses two hash functions h1(x) and h2(x) to simulate additional hash functions of the form gj(x) = h1(x) + jh2(x).
Mapping to index
Mapping output of a hash function to a bloom filter bit index requires some work. Generally, we can use the modulus (%) operator to get our bit index. For instance, you can use something like hj(x) % M where M is the number of bits in your bloom filter and hj(x) is the hash function.
Python Implementation
We are going to implement a very specific version of Bloom filter using Python which only works for a set S of integers. In this implementation,
- We defined our Bloom filter with given number of bits (
Mbitsdefault to11) parameterised by2hash functions_h1and_h2. - Hash functions
_h1takes a bits array as input and returns a new bit array created using odd numbered index bits. - Hash functions
_h2takes a bits array as input and returns a new bit array created using even numbered index bits. - Method
_hTindexmaps output of a hash function to a bit array index
#!/usr/bin/env python3
import array
class BloomFilter(object):
"""A simple BloomFilter applicable to a set S of ints"""
def __init__(self, Mbits=11):
self.Mbits = Mbits
self.abits = array.array('b', [0]) * self.Mbits
self.kHash = 2
self.Nadds = 0
def _element_index(self, element):
bitelm = bin(element)[2:]
return [self._hTindex(self._h1(bitelm), self.Mbits), self._hTindex(self._h2(bitelm), self.Mbits)]
def _h1(self, x):
"""
A simple hash function which takes bits array x as input and
returns a new bit array created using odd number index bits of x.
"""
return int("".join([v for i, v in enumerate(x) if i % 2 == 0]), 2)
def _h2(self, x):
"""
A simple hash function which takes bits array x as input and
returns a new bit array created using even number index bits of x.
"""
return int("".join([v for i, v in enumerate(x) if i % 2 == 1]), 2)
def _hTindex(self, hash, Mbits):
"""
Maps output of a hash function to a bit array index
"""
return hash % Mbits
def add(self, element):
for i in self._element_index(element):
self.abits[i] = 1
self.Nadds = self.Nadds + 1
def query(self, element):
for i in self._element_index(element):
if self.abits[i] == 0:
return False
return True
if __name__ == '__main__':
filter = BloomFilter()
S = [12000, 9000, 22011, 5551, 4953, 6582, 5929, 5662, 8888, 1382]
for element in S:
filter.add(element)
print('Is %d part of S?: %s'% (44, filter.query(44)))
print('Is %d part of S?: %s'% (9000, filter.query(9000)))
print('Is %d part of S?: %s'% (1500, filter.query(1500)))
print('Is %d part of S?: %s'% (5662, filter.query(5662)))
Let's apply double hashing technique to our basic implementation. We made some minor changes in our code,
- We added a new function to generate k hash values based on only two universal hash functions as base generators.
- We updated the
BloomFilterclass for constructor method which now accepts the number of hash functions. - We added a function to calculate the false positive probability using parameters
M,Nandk. - We added a function to calculate the size of Bloom filter in bits and compared with the size of the set S.
#!/usr/bin/env python3
import array, sys
from math import exp
class BloomFilter(object):
"""A simple BloomFilter applicable to a set S of ints"""
def __init__(self, Mbits=14, kHash=2):
self.Mbits = Mbits
self.abits = array.array('b', [0]) * self.Mbits
self.kHash = kHash
self.Nadds = 0
def _element_index(self, element):
bitelm = bin(element)[2:]
return [self._hTindex(self._hi(i, bitelm)) for i in range(self.kHash)]
def _hi(self, i, x):
"""
_hi(x) = _h1(x) + i*_h2(x)
"""
return self._h1(x) + i * self._h2(x)
def _h1(self, x):
"""
A simple hash function which takes bits array x as input and
returns a new bit array created using odd number index bits of x.
"""
return int("".join([v for i, v in enumerate(x) if i % 2 == 0]), 2)
def _h2(self, x):
"""
A simple hash function which takes bits array x as input and
returns a new bit array created using even number index bits of x.
"""
return int("".join([v for i, v in enumerate(x) if i % 2 == 1]), 2)
def _hTindex(self, hash):
"""
Maps output of a hash function to a bit array index
"""
return hash % self.Mbits
def add(self, element):
for i in self._element_index(element):
self.abits[i] = 1
self.Nadds = self.Nadds + 1
def query(self, element):
for i in self._element_index(element):
if self.abits[i] == 0:
return False
return True
def size(self):
return sys.getsizeof(self.abits)
def fp_prob(self):
return (1 - exp(-(self.kHash * self.Nadds) / self.Mbits)) ** self.kHash
if __name__ == '__main__':
filter = BloomFilter()
S = [12000, 9000, 22011, 5551, 4953, 6582, 5929, 5662, 8888]
for element in S:
filter.add(element)
print("False positive probability : %f" % filter.fp_prob())
print("Original size for S in bytes: %d" % sys.getsizeof(S))
print("Bloom filter's size in bytes: %d" % filter.size())
print('Is %d part of S?: %s'% (44, filter.query(44)))
print('Is %d part of S?: %s'% (9000, filter.query(9000)))
print('Is %d part of S?: %s'% (1500, filter.query(1500)))
print('Is %d part of S?: %s'% (5662, filter.query(5662)))
Now let's use a proper hashing function so this Bloom filter can support any data type - not just integer. We are going to use standard Python hashlib module and use hashing algorithms SHA256 and SHA224 instead of our own odd/even bit logic.
- We replaced hash functions
_h1and_h2with_sha256and_sha224respectively. - We converted input element to
stringfirst thenencoding, applyinghexdigest, and finally, we converted intoint.
#!/usr/bin/env python3
import array, sys
from math import exp
from hashlib import sha224, sha256
class BloomFilter(object):
"""A simple BloomFilter applicable to a set S of ints"""
def __init__(self, Mbits=48, kHash=9):
self.Mbits = Mbits
self.abits = array.array('b', [0]) * self.Mbits
self.kHash = kHash
self.Nadds = 0
def _element_index(self, element):
return [self._hTindex(self._hi(i, element)) for i in range(self.kHash)]
def _hi(self, i, x):
"""
_hi(x) = _h1(x) + i*_h2(x)
"""
return self._sha256(x) + i * self._sha224(x)
def _sha256(self, x):
"""
Takes any value x as input, applies SHS256 hash function and returns an int.
"""
return int(sha256(str(x).encode()).hexdigest(), 16)
def _sha224(self, x):
"""
Takes any value x as input, applies SHS256 hash function and returns an int.
"""
return int(sha224(str(x).encode()).hexdigest(), 16)
def _hTindex(self, hash):
"""
Maps output of a hash function to a bit array index
"""
return hash % self.Mbits
def add(self, element):
for i in self._element_index(element):
self.abits[i] = 1
self.Nadds = self.Nadds + 1
def query(self, element):
for i in self._element_index(element):
if self.abits[i] == 0:
return False
return True
def size(self):
return sys.getsizeof(self.abits)
def fp_prob(self):
return (1 - exp(-(self.kHash * self.Nadds) / self.Mbits)) ** self.kHash
if __name__ == '__main__':
filter = BloomFilter(Mbits=512, kHash=13)
S = '''Alabama Alaska Arizona Arkansas California Colorado Connecticut
Delaware Florida Georgia Hawaii Idaho Illinois Indiana Iowa Kansas
Kentucky Louisiana Maine Maryland Massachusetts Michigan Minnesota
Mississippi Missouri Montana Nebraska Nevada NewHampshire NewJersey
NewMexico NewYork NorthCarolina NorthDakota Ohio Oklahoma Oregon
Pennsylvania RhodeIsland SouthCarolina SouthDakota Tennessee Texas Utah
Vermont Virginia Washington WestVirginia Wisconsin Wyoming'''.split(" ")
for element in S:
filter.add(element)
print("False positive probability : %f" % filter.fp_prob())
print("Original size for S in bytes: %d" % sys.getsizeof(S))
print("Bloom filter's size in bytes: %d" % filter.size())
print('Is %s part of S?: %s'% ("Alabama", filter.query("Alabama")))
print('Is %s part of S?: %s'% ("NorthCarolina", filter.query("NorthCarolina")))
print('Is %s part of S?: %s'% ("NorthCarolina", filter.query("NorthCarolina")))
print('Is %s part of S?: %s'% ("West Delhi", filter.query("West Delhi")))
print('Is %s part of S?: %s'% ("North Sydney", filter.query("North Sydney")))
Conclusion
In this article, we discussed basics of Bloom filter. We mainly covered standard Bloom filter including some really simple implementations using Python. We lightly touched on the application and variations of Bloom filter which we will cover in upcoming posts.


