The Where's Waldo Effect in Privacy

Safeguarding individual privacy inherently means data minimisation i.e. limiting the collection and disposal of data. This principle has been a cornerstone of privacy advocacy and is even enshrined in regulations like the EU’s General Data Protection Regulation (GDPR). However, a research published by Ponte et. al (see here) is challenging this fundamental assumption, introducing what they call the “Where’s Waldo effect. They demonstrate a counterintuitive relationship between sample size and customers’ privacy risk (at least in certain scenarios).

Unveiling the Where’s Waldo Effect

The Where’s Waldo effect, cleverly named after the popular children’s book series, proposes a fascinating concept: privacy protection can actually improve with larger sample sizes. Just as Waldo becomes increasingly difficult to spot in a larger, more crowded illustration, an individual’s data becomes more protected within a larger dataset.

This finding challenges established principles like the GDPR’s emphasis on data minimisation. At first glance, this concept might seem counterintuitive, even paradoxical. How can more data collection result in better privacy? The key lies in the mathematical foundations (see here) underlying this effect.

Mathematical Magic Behind the Effect

The researchers demonstrate the Where’s Waldo effect using a sophisticated framework based on two key components: differential privacy (see here) and Generative Adversarial Networks (GANs).

Differential privacy is a mathematical approach to privacy that introduces carefully calibrated noise into data or analyses. This noise effectively masks the contribution of any single individual within the dataset. The level of privacy protection is controlled by a parameter called epsilon (ε). A smaller ε provides stronger privacy but at the cost of reduced data utility, while a larger ε allows for more accurate insights but increases privacy risk.

Here’s where the Where’s Waldo effect comes into play: for a given ε, larger datasets allow for better utility while maintaining the same level of privacy protection. In other words, more data enables the extraction of more valuable insights without increasing individual privacy risk. This is the crux of the Where’s Waldo effect - as the crowd (dataset) grows, individual privacy is enhanced rather than compromised.

The incorporation of GANs into this framework is equally innovative. GANs are a type of machine learning model consisting of two neural networks - a generator and a discriminator - that compete against each other. In this context, they’re used to generate synthetic data that closely mimics the original dataset while preserving privacy guarantees.

Seeing the Effect in Action

The power of the Where’s Waldo effect becomes evident when we look at its practical applications. The researchers demonstrated its impact in two distinct marketing scenarios: customer churn analysis and pharmaceutical prescription behavior.

In the customer churn analysis, they worked with a dataset of 1.2 million customers from a financial services company. With this full dataset, analysts could reduce privacy risk to a mere 5% increase while still deriving meaningful insights about churn patterns. However, when they reduced the sample size to just 1,262 customers, achieving comparable utility required increasing privacy risk by an astonishing 44 million percent.

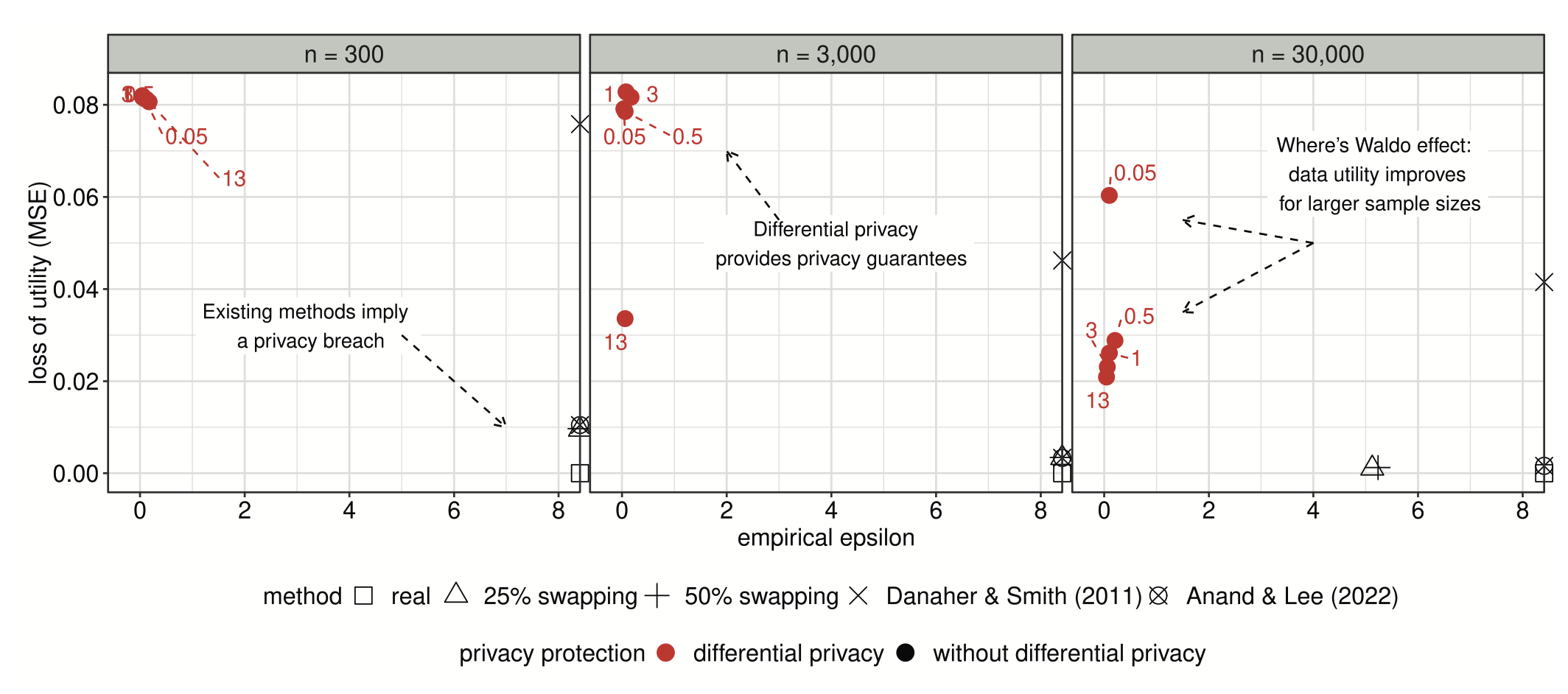
The pharmaceutical example, which analyzed physician prescription behavior over time, yielded similar results. Larger samples of physicians allowed for stronger privacy protection with less utility loss when analyzing prescription patterns. This application is particularly noteworthy as it demonstrates the effect’s validity even with complex, time-series data.

Collection vs. Protection Tradeoff

The Where’s Waldo effect challenges us to fundamentally reconsider our approach to data privacy. For years, the mantra in privacy circles has been “less is more” - the less data collected, the better the privacy protection. This research suggests that, at least in some contexts, more data can mean better privacy and better insights.

This doesn’t mean we should abandon all principles of data minimization. Rather, it suggests we need a more nuanced, mathematically grounded approach to data collection and privacy protection. We need to consider not just the amount of data we’re collecting, but how we’re protecting it, what insights we’re deriving from it, and how increasing our sample size might paradoxically enhance individual privacy.

For marketers, this could open up exciting new possibilities. It suggests that with the right privacy protections in place, we could potentially work with larger, richer datasets without increasing privacy risks. This could lead to more accurate predictive models, deeper customer insights, and more effective personalization - all while providing strong, mathematically provable privacy guarantees.

For privacy advocates and regulators, this research suggests we may need to evolve our thinking. Rather than focusing solely on data minimization, perhaps we should be equally concerned with provable privacy guarantges and responsible data use. The goal should be to find the sweet spot where we maximize both insight and privacy protection.

Challenges and Future Directions

While the Where’s Waldo effect offers exciting possibilities, it’s not without its challenges. As we look to the future, several key areas require further exploration and development.

First, there’s the issue of computational complexity. The current approach, involving differential privacy and GANs, is computationally intensive. This could limit its applicability to very large datasets or real-time analytics scenarios. Optimizing these methods for scale and speed is crucial for their widespread adoption.

Second, we need to extend this framework to handle more complex data types. While the researchers demonstrated its effectiveness with tabular and time-series data, many marketing applications involve unstructured data like text, images, or even video. Adapting the Where’s Waldo effect to these data types presents both a challenge and an opportunity.

Third, developing privacy-preserving methods that work at the point of data collection would be a significant advance. If we could apply these principles from the moment data is gathered, we could potentially eliminate the need to store raw sensitive data altogether.

Lastly, we need to deepen our understanding of how data complexity interacts with sample size requirements in this framework. Different types of analyses and different data structures may require varying levels of “crowd size” to achieve the Where’s Waldo effect. Mapping out these relationships will be crucial for practical application.

Conclusion

The Where’s Waldo effect challenges our intuitions about privacy and data. It suggests that in the world of data analytics, there’s safety in numbers. By leveraging larger datasets and advanced privacy-preserving techniques, we may be able to strike a better balance between insight and privacy.

As we move forward, it may offer a way out of the seeming deadlock between data utility and privacy protection, suggesting that with the right approach, we can have our cake and eat it too. The future of marketing analytics lies not in collecting less data, but in protecting it better.

References